NUMERI

Insiemi di numeri

Quasi tutti i numeri che compaiono nella matematica del liceo sono numeri reali. I numeri reali non sono altro che i numeri decimali che possono essere rappresentati da una successione di cifre (cioè simboli 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9), una virgola e un segno (- oppure +, e quest'ultimo in genere non si scrive esplicitamente).
Esempi di numeri reali sono -5 (''meno cinque''), 54,321 (''cinquantaquattro virgola tre due uno'') e numeri la cui rappresentazione decimale non ha termine, perchè:

le cifre si ripetono periodicamente (come -0,33333333... e 34,12121212...; in tal caso si chiamano periodici), oppure
vi è un altro tipo di regolarità (come 0.101001000100001...) oppure
non vi è regolarità evidente, come nel caso del famoso Pi greco ($\pi$ = 3.14159265...) che indica il rapporto fra circonferenza e diametro in un qualsiasi cerchio.

L'insieme di tutti i numeri reali si indica con $\mathbb{R}$.

In un certo senso possiamo immaginare i numeri reali anche come oggetti geometrici, cioè come punti su una retta. Chiamiamo due punti di questa retta reale 0 e 1 e raffiguriamo l'insieme $\mathbb{R}$ dei numeri reali come nel diagramma seguente, dove abbiamo riportato alcuni numeri reali con una marcatura:

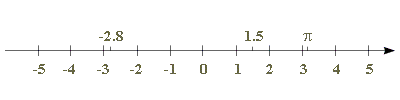
Possiamo pensare a un nastro di lunghezza infinita con marcatura talmente fine da permettere misurazioni infinitamente precise.

Alcuni sottoinsiemi di $\mathbb{R}$ sono particolarmente importanti:

I numeri naturali sono i numeri che si usano per contare: 1, 2, 3, 4,... Sono esattamente quei numeri reali positivi la cui rappresentazione decimale termina dopo la virgola, cioè contiene soltanto zeri ( 5 coincide con 5.0000...) L'insieme di tutti i numeri naturali si indica con $\mathbb{N}$:

$\mathbb{N} = \{1, 2, 3, 4, ...\}$ (1)

Sulla retta reale esso forma una successione di punti a distanza 1, partendo da 1 verso destra.

A volte può essere utile iniziare a contare da 0. Aggiungendo lo zero all'insieme dei numeri naturali si ottiene

$\mathbb{N}$₀$= \mathbb{N} \cup \{0\} =\{0,1, 2, 3, 4, ...\}$ (2)

Attenzione: In alcuni libri i numeri naturali partono da zero e l'insieme dei numeri naturali $\mathbb{N}$ indica quello che noi abbiamo chiamato $\mathbb{N}_0$ .

I numeri interi sono quei numeri reali la cui rappresentazione decimale termina dopo la virgola, cioè contiene soltanto zeri. L'insieme dei numeri interi si indica con $\mathbb{Z}$ :

$\mathbb{Z} = \{..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...\}$ (3)

Sulla retta reale esso forma una successione di punti a distanza 1, partendo da 0 verso destra e sinistra.

I numeri razionali sono quei numeri reali la cui rappresentazione decimale da un certa cifra in poi consiste soltanto di zeri oppure diventa periodica (Esempi: 0.4 e - 11.2181818...). Si dimostra che essi sono esattamente quei numeri reali che possono essere rappresentati come quoziente di un numero intero per un altro numero intero (diverso da 0). (Ad esempio. -11.2181818... coincide con -617/55). I numeri razionali sono quindi le frazioni di forma "numero intero/numero intero". Li possiamo scrivere come frazioni o con la loro rappresentazione decimale. Per un numero come $\frac{2}{3}$ (che coincide con 0.6666... ) sarà preferibile la forma come frazione. L'insieme dei numeri razionali si indica con $\mathbb{Q}$.
Sulla retta reale esso forma un insieme di punti estremamente "densi": fra due numeri razionali è sempre possibile trovarne un terzo (anzi, un numero infinito di altri numeri razionali).

I numeri irrazionali sono quei numeri reali che non sono razionali. Cioè quelli la cui rappresentazione decimale non termina ne è periodica (Esempi: 0.1010010001000001... oppure p), sono quindi quelli che non possono essere scritti come quoziente di due numeri interi. L'insieme dei numeri irrazionali può essere indicato con $\mathbb{R} \setminus \mathbb{Q}$: l'insieme degli elementi di $\mathbb{R}$ che non sono contenuti in $\mathbb{Q}$.

Osservazioni su Q.

Sull'insieme dei numeri reali abbiamo le strutture algebriche Addizione e Moltiplicazione, connesse fra loro dalla regola

$2 \times (4+6)=2 \times 4 + 2 \times 6$ (4)

detta "legge distributiva". L'operazione di addizione dà luogo (in un certo senso come "inversione") a un'altra operazione, la sottrazione. Analogamente la moltiplicazione da luogo alla divisione.

A differenza della sottrazione, dobbiamo fare una restrizione importante per la divisione: non è permesso dividere per zero. Infatti la domanda fondamentale su cui si basa la divisione è: 0 × quanto = 1? Ma moltiplicare un numero per 0 da sempre 0, e quindi mai 1! Interpretando la divisione come "l'inverso" della moltiplicazione vediamo che la divisione per 0 non è definita.

Divisibilità

Un concetto importante nell'ambito dei numeri naturali è il concetto di multiplo. Ad esempio 12 è un multiplo di 3 (il quadruplo) poichè la divisione $12/3$ ci da il risultato intero 4. Diremo anche che "3 divide oppure è un divisore di 12".

5 non è un divisore di 21 poichè $21/5$ non è un numero intero. In altre parole, 21 non è un multiplo di 5: non esiste un numero intero $n$, tale che 21 = 5 · n. Possiamo però esprimere 21 come 21 = 5 · 4 + 1. Il numero 1 è il resto della divisione di 21 per 5.

La divisibilità si estende in maniera ovvia anche ai numeri relativi (ad esempio, 3 è un divisore di -12). Un numero intero si dice pari se possiede 2 come divisore, altrimenti si dice dispari.

Ogni numero intero possiede se stesso ed il numero 1 come divisore. Un numero naturale che non possiede altri divisori oltre a questi due (1 e se stesso) si dice primo. Ad esempio 7 è un numero primo poichè nessuno dei numeri 2, 3, 4, 5 e 6 è suo divisore, e naturalmente neanche i numeri maggiori di 7 sono suoi divisori. L'elenco dei numeri primi inizia così 2, 3, 5, 7, 11, 13,17, 19, 23, ...

Con i numeri primi possiamo "costruire" tutti i numeri naturali. Ciascun numero naturale può essere scritto in maniera univoca come prodotto di numeri primi.

Esempio: il numero 18 può essere scritto come prodotto 2 · 9. Il fattore 9 può essere ulteriormente scomposto come 3 · 3, per cui si ha 18 = 2 · 3 · 3. Un'ulteriore scomposizione non è possibile poichè 2 e 3 sono numeri primi. Questa è la scomposizione in fattori primi di 18. i numeri 2 e 3 si chiamano fattori primi oppure divisori primi. (Il fattore 2 compare solo una volta, mentre 3 compare due volte. Si parla di molteplicità di un fattore primo). Abbreviando 3 · 3 = 3² possiamo scrivere la scomposizione in fattori primi di 18 come:

18=2 · 3² (5)

Si dimostra che ogni numero naturale possiede solo una scomposizione in fattori primi (cioè che essa è univoca).

Già nell'antichità era noto che esiste un numero infinito di numeri primi.

Dimostrazione.

L'ordinamento dei numeri reali: $<$, $\le$, $>$ e $\ge$

Se abbiamo due numeri reali, uno è sempre minore dell'altro (quindi l'altro maggiore del primo). Se pensiamo alla retta reale possiamo dire che un numero è minore di un altro se giace alla sua sinistra. Quindi -5 è minore di 3 (e 3 è maggiore di -5), in simboli:

$ -5 < 3$ $3 > -5$ (6)

Possiamo anche esprimere che un numero reale è minore oppure uguale ("minore-uguale") di un altro (cioè che l' altro è maggiore oppure uguale, cioè "maggiore-uguale" del primo) scrivendo

$3 \leq 5$ $4 \leq 4$ $5 \geq 3$ $4 \geq 4$ (7)

Questi simboli sono utili quando vogliamo descrivere sottoinsiemi dell' insieme $\mathbb{R}$ dei numeri reali. Ad esempio:

$\mathbb{R}$⁺$=\{ x \in \mathbb{R} \mid x > 0\}$ (8)

e l'insieme di tutti i numeri reali positivi è

$\mathbb{R}$₀⁺ $=\{ x \in \mathbb{R} \mid x \ge 0\} =\{0\} \cup \mathbb{R}$⁺ (9)

è l'insieme di tutti i numeri reali non negativi. In altre parole, sulla retta reale $\mathbb{R}$⁺ è l'insieme di tutti i punti che giacciono a destra rispetto a 0 (escluso lo 0), mentre $\mathbb{R}$₀⁺ comprende anche 0.

I sottoinsiemi connessi di $\mathbb{R}$ (cioè della retta reale) si chiamano intervalli. Si indicano con parentesi tonde ( ) o quadre [ ] distinguendo intervalli aperti (quando non comprendono gli estremi), ad esempio:

$(-1, 2) = \{ x \in \mathbb{R} \mid -1 < x < 2\},$ (10)

e intervalli chiusi (quando comprendono gli estremi), ad esempio

$[-1, 2] = \{ x \in \mathbb{R} \mid -1 \leq x \leq 2 \}$ (11)

oppure semichiusi come:

$(-1, 2] = \{ x \in \mathbb{R} \mid -1 < x \leq 2\}$ (12)

Un intervallo può anche essere illimitato, come:

$\mathbb{R}$⁺$=(0,\infty)$ e $\mathbb{R}$₀⁺$=[0,\infty)$ (13)

dove $\infty$ sta a indicare "infinito". Ecco un esempio di intervallo illimitato a sinistra:

$(-\infty,3]=\{ x \in \mathbb{R} \mid x\leq 3\}$ (14)

Il valore assoluto

Il valore assoluto di un numero reale si ottiene "ponendo il segno del numero sul +". Si indica con il simbolo $\mid \mid$ . Esempi:

$\mid 5.1 \mid=5.1$ $\mid -7.3\mid=7.3$ $\mid \pi \mid =\pi$ $\mid -\pi \mid =\pi$

Al numero 0 si assegna il valore assoluto 0, quindi: $\mid 0 \mid = 0$.

Sulla retta reale il valore assoluto è la distanza (sempre $\geq 0$) di un numero dallo zero. Una grandezza come $\mid 12.1 - 13.1 \mid$ misura la distanza (positiva) fra i due punti 12.1 e 13.1 della retta reale (che in questo caso è pari a 1). Questo tipo di notazione è utile quando si vuole esprimere che due numeri sono vicini l'uno all'altro (senza entrare nel merito su quale è maggiore dell'altro).

Definizione valore assoluto.

Potenze

Le potenze sono innanzitutto una maniera di indicare la moltiplicazione multipla di un numero con se stesso. Ad esempio:

$5$²$=5\times5=25$ $5$³$=5\times5\times5=125$ $5$⁴$=5\times5\times5\times5=625$ (15)

("5 al quadrato" oppure "5 alla seconda", "5 al cubo" oppure "5 alla terza", "5 alla quarta"). Poniamo inoltre:

$5$¹$= 5$ e $5$⁰$= 1$ (16)

(nel primo caso 5 compare una volta sola, nel secondo non compare affatto, quindi 0 volte). I numeri scritti in alto si chiamano esponenti. Al posto di 5 possiamo ovviamente mettere qualsiasi numero reale.

Le regole per la moltiplicazione implicano $0^2= 0^3 =...0$. Ecco due esempi di potenze di numeri negativi:

$(-5)^2 = 25$ $(-5)^3 = -125$ (17)

Due segni negativi "si neutralizzano", per cui la potenza di un numero negativo è positiva (negativa) quando l'esponente è pari (dispari).

Da ciò segue:

Il quadrato di un numero reale è sempre $\geq 0$.
Il quadrato di un numero diverso da zero è sempre $> 0$.

La potenza di una frazione si calcola elevando a potenza numeratore e denominatore :

(2/3)² = 2²/3² = 4/9 (18)

Ciò segue dalle regole per la moltiplicazione di due frazioni.

In tutti questi esempi gli esponenti sono numeri naturali (oppure 0). Esistono anche potenze con esponente negativo oppure non-intero. Di questo parleremo in un capitolo successivo.

Radici

Per adesso,fondamentalmente, abbiamo soltanto parlato di regole di calcolo. Passiamo ora a un primo "vero" problema matematico: dato un numero reale positivo, esiste un numero reale il cui quadrato è il numero dato?

Primo esempio: iniziamo con il numero 4. Esistono addirittura due soluzioni al nostro problema, -2 e 2. Quella positiva si chiama radice (o meglio, radice quadrata) di 4, in simboli:

√4 = 2 (19)

Analogamente √9 = 3, √16 = 4, √25 = 5 ecc.

Altro esempio: esiste un numero reale, il cui quadrato è 2? Invece di una dimostrazione rigorosa, preferiamo discutere intuitivamente: poichè 1² =1<2, il numero 1 "è troppo piccolo" per essere preso in considerazione come √2. Aumentiamolo un po': 1.01² = 1.0201 < 2, quindi 1.01 è ancora troppo piccolo. Continuiamo ad aumentarlo a piccoli passi. Quando avremo raggiunto 1.5, il nostro calcolo 1.5² = 2.25 > 2 ci mostrerà che abbiamo già oltrepassato la meta: il numero 1.5 è troppo grande per essere √2. Adesso pensiamo di cominciare da 1 e aumentare il numero non a piccoli passi, ma continuamente, fino a raggiungere il numero 1.5 (immaginiamo quindi di muovere un punto sulla retta reale spostandolo da 1 verso destra fino a 1.5). In un qualche punto fra 1 e 1.5, troveremo un numero il cui quadrato è 2. Questa osservazione è basata sul fatto che piccole variazioni del numero implicano solo piccole variazioni del suo quadrato (nel linguaggio matematico ciò si esprime dicendo che calcolare il quadrato è una funzione continua).

Concludiamo (e ciò si può dimostrare rigorosamente): esiste esattamente un numero reale positivo il cui quadrato è 2. Si chiama la radice (più precisamente, la radice quadrata) di 2 e si indica con √2. Essa si trova fra 1 e 1.5. Abbiamo inoltre che anche il quadrato di -√2 è 2 (perchè calcolando il quadrato il segno negativo scompare). -√2 si trova fra -1.5 e -1.

La rappresentazione decimale di √2 è 1.41421... Per indicare il numero con esattezza dobbiamo usare il simbolo √2. Non c'è ragione di sostituirlo con un valore approssimato come 1.4142.

Lo stesso argomento vale per per qualsiasi numero reale positivo: esistono sempre due numeri (distinti solo dal segno) il cui quadrato è il numero dato. Quello positivo viene detto radice. Così si definiscono le radici √3, √1.5 e √π (il cui valore approssimato può essere determinato con un calcolatore).

Il numero 0 è un caso limite. Qui abbiamo solo un numero il cui quadrato è 0, lo 0 stesso. Quindi √0 = 0.

Si noti che non esiste però alcun numero reale il cui quadrato sia un numero negativo. Infatti abbiamo visto prima che il quadrato di qualsiasi numero reale è sempre $\ge 0$. (Esiste un concetto di numero più generale, i cosiddetti "numeri complessi", che permette di estrarre la radice anche da numeri negativi).

Solo raramente la radice di un numero naturale è un numero naturale. Ciò vale per i "numeri quadrati" 1, 4, 9, 16, 25, 36, 49, 64, ... . Negli altri casi le radici sono irrazionali.

Già nell'antichità era noto che √2 è un numero irrazionale.

Dimostrazione.

Per motivi che capiremo più avanti, le radici quadrate vengono a volte scritte come potenze con esponente 1/2:

$16^{1/2} =\sqrt{16}=4$ (20)

Due regole per il calcolo con le radici:

La radice di un prodotto è il prodotto delle radici, ad esempio $\sqrt{4\cdot 9}=\sqrt{4}\cdot \sqrt{9}$ (si verifichi!).
La radice di una frazione si calcola estraendo la radice da numeratore e denominatore:

$$\sqrt{\frac{4}{9}}=\frac{\sqrt{4}}{\sqrt{9}}= \frac{2}{3}$$ (21)

Ciò segue dalla regola 1 e dalle regole per la moltiplicazione di frazioni.

Menzioniamo infine le radici n-esime. Ad esempio, la radice quarta di 17 è quel numero reale positivo la cui quarta potenza è 17. La sua rappresentazione decimale è 2.03054... La radice terza è anche detta radice cubica.