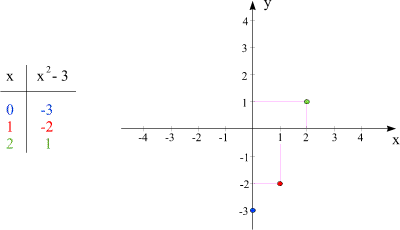FUNZIONI

Che cos'è una funzione?

Funzioni come Input-Output

Le funzioni (anche dette applicazioni) sono uno dei concetti più importanti della matematica. Non solo in matematica, ma anche in quasi tutte le applicazioni hanno un ruolo fondamentale. Questa applicabilità universale risale alla semplicità dell'idea che ne sta alla base.

Allora che cos'è una funzione? Possiamo intenderla come un apparecchio di Input- Output. Prende un oggetto come Input e fornisce un oggetto come Output. E questo avviene secondo una prescrizione precisa (univoca) - gli stessi Input daranno sempre gli stessi Output.

Per noi "oggetto" per adesso significa "numero". Quindi una funzione per noi per ora è un calcolatore che prende un numero come Input e lo trasforma in un numero come Output. Ecco un calcolatore del genere:

Si inserisca un numero e si clicchi. Si provi con un altro numero. Prima di continuare, si ripeta questo procedimento diverse volte e si cerchi di scoprire come vengono trasformati i numeri inseriti.

Avrete già capito: Il calcolatore eleva al quadrato il numero dato. È un calcolatore del quadrato. L'idea è di assegnare a ciascun numero x il suo quadrato x² . La prescrizione è dunque "elevare al quadrato". Così abbiamo definito una funzione. Potremmo chiamarla "funzione quadrato".

La prescrizione è univoca: gli stessi Input daranno sempre gli stessi Output, come già detto sopra. Potremmo adesso chiederci se vale anche il contrario, se dall'Output possiamo risalire all'Input. Se l'Output è il numero 4 - cos'era l'Input? Se rispondiamo "il numero 2", non abbiamo completamente ragione - potrebbe essere anche stato -2! Risalire all'Input non è sempre possibile! Le due caselle nel nostro calcolatore del quadrato non sono "equiparate". Se conosciamo il valore della casella di sinistra (Input), conosciamo anche il valore della casella di destra (Output), sarà il quadrato dell'Input. Ma dalla casella destra non possiamo necessariamente ricavare il valore della casella sinistra. Le funzioni lavorano quindi in una "direzione".

Input $\longrightarrow$ Output

che abbiamo indicato con una freccia nel nostro calcolatore.

Guardiamo adesso un'altro esempio nel nostro calcolatore:

Si cerchi di scoprire come vengono trasformati i numeri inseriti.

Scoperto? La macchina raddoppia il numero di Input e sottrae 1. La prescrizione adesso è " raddoppia e sottrai 1". Si tratta quindi della funzione "raddoppia e sottrai 1".

Abbiamo visto per ora due funzioni:

La prima assegna a ciascun numero x il numero x²,

la seconda assegna a ciascun numero $x$ il numero $2 x - 1$.

Per non dovere ripetere ogni volta queste righe, daremo loro un nome. Chiamiamo la prima $f$ e la seconda $g$. Abbiamo quindi:

La funzione $f$ assegna a ciascun numero x il numero x²,

La funzione $g$ assegna a ciascun numero $x$ il numero $2 x - 1$.

In matematica si usano altre due notazioni più concise per caratterizzare le funzioni.

La notazione con la freccia

Consiste nel mettere due punti dopo il nome della funzione ed esprimere la "prescrizione" con una freccia:

$ f: x \longrightarrow $x² (1)

Rivediamo il nostro calcolatore del quadrato in questa veste:

Adesso si vede chiaramente che cosa succede (o meglio, come agisce la funzione). Nella casella di sinistra c'è un numero qualsiasi x, nella casella di destra il suo quadrato x².

Analogamente si descrive l'azione della funzione $g$ come

$g : x \longrightarrow 2x-1$ (2)

Oltre alla notazione con la freccia si usa anche un'altra notazione che in pratica è anche più utile.

La notazione con parentesi

Consideriamo nuovamente la funzione f : x $\rightarrow$ x² che calcola il quadrato del numero di Input. Ovviamente l'Output dipende dall'Input. Spesso si vuole esprimere ancora più semplicemente questa dipendenza nella notazione indicando l'azione della funzione in forma:

f(x)=x² (3)

Si legge così: "f di x è uguale a x²". Così si può scrivere in forma compatta l'azione di $f$ sul numero 3: lo trasforma in $f(3)$ (che è il quadrato di 3 e quindi 9).

Questo uso delle parentesi non va scambiato con l'uso delle parentesi per raccogliere simboli. Le parentesi in (x + 1)² hanno un significato completamente diverso da quelle in $f(3) = 9$ oppure in (3).

Il simbolo utilizzato non ha nessuna importanza e invece di (3) possiamo caratterizzare $f$ in forma:

f(s)=s² (4)

Per illustrare questa notazione, ci vogliamo domandare che cosa è $f(f(3))$. Non è difficile: qui applichiamo $f$ al numero 3 e poi applichiamo di nuovo $f$ al risultato. L'output della prima applicazione è $f(3) = 9$, quindi $f(f(3)) = f(9) = 81$.

La nostra funzione $g$ può essere caratterizzata analogamente in forma:

$g(x)=2x-1$ (5)

Un esempio dell'azione della funzione su un numero: $g(8) = 2 \times 8 - 1 = 15$.

La dipendenza di una grandezza dall'altra espressa da questa notazione è un aspetto importante del concetto di funzione. Quando il valore di una grandezza $y$ dipende dal valore di un'altra grandezza $x$ (troveremo degli esempi concreti più avanti), la grandezza dipendente $y$ viene scritta spesso come $y(x)$, cioè il simbolo $y$ viene utilizzato simultaneamente come nome di una grandezza (variabile) e di una funzione. (La grandezza dipendente $y$ corrisponde all'"Output", quella indipendente $x$ all' "Input").

La definizione generale di funzione

Si possono considerare funzioni anche per oggetti matematici diversi dai numeri. In generale per definire una funzione avremo bisogno di due insiemi che vogliamo chiamare A e B.

Definizione:una funzione (anche detta applicazione) $f$ "dall'insieme A all'insieme B" è una prescrizione che assegna a ciascun elemento di A in maniera univoca un elemento dell'insieme B. Ciò si esprime scrivendo $f$

$f: A \rightarrow B$ (6)

Inoltre è necessario descrivere la prescrizione (non importa in quale notazione o linguaggio) affinchèè sia chiaro come la funzione agisce su un elemento arbitrario dell'insieme A. L'insieme A è detto dominio di $f$ , l'insieme B è detto codominio di $f$.

Per adesso nei nostri esempi si aveva A = B = $\mathbb{R}$, l'insieme dei numeri reali. Per molte delle funzioni che impareremo a conoscere l'insieme A (da cui possono scelti i valori di Input) sarà un sottoinsieme di $\mathbb{R}$. I valori di Output saranno quasi sempre numeri reali, cioè B = $\mathbb{R}$. In questo caso si parla di funzioni reali.

A che cosa servono le funzioni?

Ogni volta che il valore di una grandezza dipende dal valore di un'altra grandezza, si ha una funzione. La natura e la nostra vita sono piene di questo tipo di dipendenze, e così un numero incommensurabile di processi e connessioni può essere descritto, modellato e compreso nel linguaggio matematico delle funzioni - a volte con grande precisione sotto forma di teorie molto evolute, altre volte soltanto in forma di rozze approssimazioni.

Si consideri ad esempio un termometro appeso da qualche parte. La temperatura segnata non sarà sempre la stessa, ma varierà con il tempo, ad esempio con l'escursione termica giornaliera o stagionale. In altre parole, la temperatura dipende dall'istante in cui viene misurata. Ciò rappresenta una funzione: in un dato istante $t$ (Input) viene segnata una certa temperatura T (Output). Diremo che "la temperatura è una funzione del tempo". Come abbiamo visto sopra si può usare il simbolo dell'Output (qui T ) come nome della funzione. A ciascun istante $t$ il termometro (as)segna la temperatura $T(t)$. Qualsiasi termometro concreto che vi viene in mente definisce una tale funzione. Che la temperatura sia da calcolare con una determinata procedura o che sia semplicemente da leggere non fa differenza - in ogni caso si tratta di una funzione, perchè ad ogni istante $t$ corrisponde una certa temperatura T.

Altri esempi.

Come definire una funzione

Abbiamo visto prima varie maniere di scrivere una funzione (notazione con la freccia, notazione con le parentesi). Si trattava di considerazioni di carattere formale, adesso vogliamo invece discutere come possiamo descrivere l'azione di una funzione matematicamente.

Abbiamo già visto due esempi di funzioni: una funzione $f$ la cui azione è f(x) = x², e una funzione $g$ la cui azione è $g(x) = 2x - 1$. Entrambi sono definite da un'espressione. Potremmo anche definire una funzione $h : \mathbb{R} \rightarrow \mathbb{R}$ tramite:

$h(x) = x (x-4)$ (7)

Come per $f$ e $g$, si tratta di una prescrizione univoca che assegna a ciascuna variabile indipendente (la $x$) un valore $f(x)$. Ecco il "calcolatore" di Input-Output corrispondente:

Si controlli che il calcolatore assegna davvero a ciascun x il valore x · (x - 4)².
(Si provi a inserire $x = 4$. Perchèè il risultato è 0? In quanto 4(4 - 4)² = 0)

Analogamente si vede che qualsiasi espressione (che dipende da un'unica variabile) definisce una funzione!

Ma attenzione: non tutte le espressioni definiscono una funzione $\mathbb{R} \rightarrow \mathbb{R}$!!! Se per certi valori della variabile l'espressione non è definita, bisogna restringere il dominio della funzione corrispondente. Vi presentiamo qui di seguito due esempi:

x $\rightarrow$ 1/x
x $\rightarrow $√x (funzione radice)

I 2 esempi.

Non tutte le espressioni definiscono una funzione $\mathbb{R} \rightarrow \mathbb{R}$!!!

Quando una funzione è data da un'espressione che non è definita per tutti i numeri reali, bisogna ridurre il suo dominio appropriatamente.

Ad esempio l'espressione 1/x non è definita per $x = 0$. Quindi la funzione u(x) = 1/x non è definita per $x = 0$ . Dobbiamo quindi considerare u non come funzione $\mathbb{R} \rightarrow \mathbb{R}$, ma come funzione
$\mathbb{R}* \rightarrow \mathbb{R}$
con $\mathbb{R}*$ l'insieme dei numeri reali diversi da zero.
Anche per x $\rightarrow$ √x (la funzione radice) è necessaria una restrizione in quanto la radice di un numero reale negativo non è definita. Dobbiamo quindi considerare la funzione radice come funzione
$\mathbb{R}$₀⁺ $\rightarrow \mathbb{R}$
con $\mathbb{R}$₀⁺ l'insieme dei numeri reali non negativi (cioè i positivi e lo zero).

Le funzioni viste per ora sono tutte descritte da un'espressione in cui si applicano operazioni elementari (o da loro derivate, come la radice) alla variabile $x$. Esistono però anche funzioni, la cui azione è facilmente comprensibile, ma per le quali non è facile (o addirittura non è possibile) trovare una tale descrizione.

Ecco quattro esempi di funzioni che non sono definite da un'espressione:

Sia $k : \mathbb{R} \rightarrow \mathbb{R}$ la funzione che a ciascun $x$ positivo assegna $x$ e a tutti gli altri valori di $x$ assegna il numero 0. In linguaggio formale:
$$ k(x)=\left\{ \begin{array}{ll} x &\hbox{ se }x>0\\ 0 &\hbox{ se }x \leq 0. \end{array}\right. $$
Sia $q : \mathbb{R} \rightarrow \mathbb{R}$ la funzione che a ciascun numero razionale $x$ assegna 1 e a ciascun numero irrazionale $x$ assegna 0. In linguaggio formale:
$$ q(x)=\left\{ \begin{array}{ll} 1 &\hbox{ se }x\in \mathbb{Q}\\ 0 &\hbox{ se }x \notin \mathbb{Q}. \end{array}\right. $$
Sia $p : \mathbb{N} \rightarrow \mathbb{N}$ la funzione che ad ogni numero naturale $n$ assegna l'ennesimo numero primo, cioè:

Per ciascun $n$ sia $p(n)$ l'$n$-esimo numero primo

L'elenco dei numeri primi inizia così: 2, 3, 5, 7, 11, 13... Quindi p(1) = 2, p(2) = 3, p(3) = 5, p(4) = 7 ecc. Da secoli si cerca invano di trovare un'espressione semplice per rappresentare questa funzione, ma molto probabilmente tale espressione non esiste.
Come ultimo esempio menzioniamo la funzione valore assoluto. Ad ogni numero reale $x$ essa assegna il suo valore assoluto
$$ |x|=\left\{ \begin{array}{ll} x &\hbox{ se }x\geq 0\\ -x &\hbox{ se }x <0. \end{array}\right. $$
Si tratta quindi della funzione $x \rightarrow \mid x\mid$.

Questi esempi ci mostrano che quello che conta quanto si definisce una funzione è l'univocità della prescrizione. Che questa sia realizzata da una semplice espressione, da una distinzione di vari casi, o che possa soltanto essere espressa in parole, non è tanto importante. Qui vediamo la differenza essenziale fra espressioni e funzioni.

Tabelle dei valori

Data una funzione, cioè una prescrizione per assegnare a un numero (che chiameremo $x$) un valore, può essere necessario avere una visione d'insieme della sua azione. Ad esempio può essere rilevante sapere per quali $x$ essa assume il valore zero oppure conoscere il segno dei valori della funzione quando $x$ è un numero molto grande.

Una prima possibilità è data dalla tabella dei valori. Ciò significa che si riportano in una tabella vari valori di $x$ con i valori della funzione corrispondenti, cioè vari esempi dell'azione della funzione.

Lo esemplifichiamo per la funzione $g$ data da $g(x) = 2x - 1$. Si scelga il passo con cui procedere per sostituire la $x$ (per esempio 1) nella casella apposita e si clicchi "produrre la tabella"!

Si otterranno 17 valori per $x$ la cui distanza sarà data dal passo scelto, insieme ai rispettivi valori della funzione. Accanto ad ogni numero $x$ nella colonna di sinistra si trova il valore $2x - 1$ nella colonna di destra. Si faccia qualche prova!

Si scelgano anche passi diversi, ad esempio 100,10, 0.5, 0.1 e 0.01 !

Si usi questa tabella interattiva per rispondere alle seguenti domande:

Dove (cioè per quali $x$) il valore della funzione diventa zero? (Si usi successivamente il passo 1 e 0.1. Quale scelta è più adeguata per rispondere alla domanda?)
Dove (cioè per quali $x$) è positiva la funzione?
Come agisce - approssimativamente - la funzione quando $x$ è molto grande? (Si scelga il passo 1000 !)

Risposte.

Tali colonne di numeri però non sono molto chiare. C'è un metodo molto migliore, per vedere proprietà importanti di una funzione in un colpo d'occhio, il metodo grafico di cui parleremo adesso.

Il grafico di una funzione

Preparativi:Rappresentazione grafica della tabella dei valori

Ogni riga nella tabella dei valori (vedi sopra) è composta da una coppia di numeri: un valore per la variabile indipendente (che come il solito chiameremo $x$) insieme al valore assegnato dalla funzione. Tali coppie di numeri possono essere rappresentate graficamente come punti di un piano.

Ricordiamo che nel piano possiamo introdurre due assi ortogonali. La posizione di un punto sarà poi data da due numeri (le sue coordinate). Chiamando gli assi rispettivamente asse delle $x$ ("ascisse") e delle $y$ ("ordinate"), la posizione di un punto è data da una coppia $(x, y)$ di coordinate, e viceversa ciascuna coppia di numeri descrive un punto.

Le coppie di numeri che compaiono nella tabella dei valori di una funzione $f$ hanno sempre la forma

$(x, f(x))$ (8)

Vogliamo interpretare questa coppia come coordinate di un punto nel piano. Per ciascun valore di $x$ si definisce come $y$ il valore della funzione corrispondente. Così ogni riga della tabella dei valori diventa un punto del piano, e la tabella corrisponde a un insieme di punti.

Ecco un esempio concreto. Definiamo

$f(x)=x^2 - 3$ (9)

quindi $f$ è la funzione che assegna a ciascun numero reale $x$ il numero $x^2 - 3$. Costruiamo una piccola tabella dei valori scegliendo per $x$ i numeri 0, 1 e 2. La vedremo a sinistra nella prossima figura. La prima riga (blu) corrisponde alla coppia di numeri (0,-3), la quale corrisponde al punto con l'ascissa 0 e l'ordinata -3. Nella figura lo troverete a destra (indicato in blu). La seconda riga (rossa) e la terza riga (verde) della tabella corrispondono agli altri due punti riportati nella figura.

Si controllino i tre valori della funzione (-3, -2 e 1) e la posizione dei tre punti!
La tabella dei valori contiene la stessa informazione che la posizione dei tre punti. Data la tabella, possiamo disegnare i tre punti. Viceversa, se conosciamo solo la parte destra della figura, possiamo ricostruire la tabella dei valori leggendo le coordinate. Il sistema cartesiano con i tre punti riportati non è altro che una rappresentazione grafica della tabella dei valori.

Consideriamo adesso la stessa funzione con una tabella dei valori più ampia.

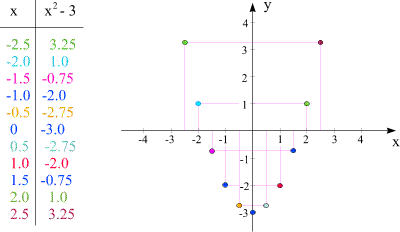
grafico

Le coppie di numeri nella tabella hanno lo stesso colore dei punti corrispondenti nel sistema di coordinate $x-y$. Si controlli la loro posizione!

Sopprimendo i numeri lungo gli assi e le linee ausiliarie otteniamo

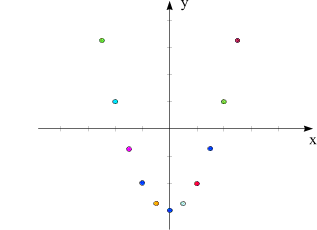
grafico

Adesso che la tabella dei valori ha un numero più consistente di dati, la "funzione comincia ad assumere una forma". Con queste "forme" si lavora molto spesso in matematica.

Riassumiamo che cosa ci mostra questo esempio:

In parole povere, si disegna il grafico di una funzione riportando per i punti sull'asse delle $x$ il valore corrispondente della funzione "in alto" (oppure "in basso, se esso è negativo).

Più brevemente: $x$ si riporta orizzontalmente, $f(x)$ si riporta verticalmente. È dall'asse delle $x$ che sceglieremo i valori per la variabile indipendente $x$.

Viceversa, un punto con le coordinate $(x, y)$ nel piano rappresenta graficamente l'azione della funzione sul valore di input $x$. Possiamo leggere il valore $f(x)$ come ordinata $y$ del punto.

Il grafico di una funzione

Le tabelle dei valori hanno il difetto di contenere solo un certo numero di valori per $x$. Perciò la tabella dei valori contiene sempre meno informazione che la funzione stessa. Per ovviare a questo problema, definiamo adesso un oggetto geometrico che tiene conto di tutti i possibili valori di $x$.

Definizione: Il grafico di una funzione $f : \mathbb{R} \rightarrow \mathbb{R}$ è l'insieme di tutte le coppie $(x, f(x))$.
$\mathbb{R}$ è come sempre l'insieme dei numeri reali. La funzione $f$ associa un valore a ciascun numero reale e il grafico è l'insieme di tutte le coppie

(variabile indipendente, valore associato).

Nella notazione della teoria degli insiemi:

$\{(x,f(x) | x \in R\}$ (10)

Si ricordi il significato di questa notazione! Si legge "l'insieme di tutte le coppie $(x, f(x))$ per le quali $x$ è elemento di $\mathbb{R}$".

Poichè il piano è l'insieme di tutte le coppie di numeri, il grafico di una funzione può essere considerato un sottoinsieme del piano. Per quasi tutte le funzioni che ci interessano si tratta di una curva (una retta oppure una linea curva).

Riguardiamo l'esempio della funzione $f$ data da $f(x) = x^2 - 3$. Ecco il suo grafico:

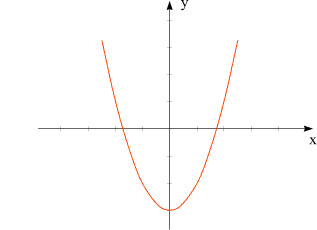
grafico
Lo si confronti con la rappresentazione grafica della tabella dei valori che avevamo riportato sopra! Ogni riga della tabella corrisponde a un punto sulla curva.
Quest'ultima, fra l'altro, è una parabola - la ritroveremo più avanti.

Sullo schermo (o anche in un disegno reale) il grafico di una funzione non è altro che la rappresentazione grafica di una grande tabella di valori. Si pensi di avere a disposizione una tabella di $f$ con duecento valori di $x$ compresi fra $x = -2.5$ e $x = 2.5$ e di riportare ogni riga della tabella come puntino rosso (Pixel) in un diagramma: il risultato sembrerà una curva. Questo aspetto pratico del grafico va distinto dal suo significato matematico esatto - come insieme di tutte le coppie $(x, f(x))$. Per quasi tutte le funzioni con cui avremo a che fare il grafico è una linea continua - diversamente dalla rappresentazione grafica della tabella dei valori che, invece di continua, viene detta struttura discreta.

L' equazione di una funzione

C'è una notazione alternativa a (10) molto importante. Per le coordinate $x$ e $y$ di ciascun punto del grafico di una funzione abbiamo $y= f(x)$. Lo possiamo quindi scrivere come:

$\{ (x, y) \in \mathbb{R}^2 \mid y = f (x) \}$ (11)

cioè come insieme di tutti i punti del piano che soddisfano l'equazione:

$y=f(x)$. (12)

La chiameremo equazione della funzione. È un'equazione nelle due variabili $x$ e $y$. Ogni punto con le coordinate $(x, y)$, per il quale essa è verificata appartiene al grafico di $f$. (Il grafico appare qui come insieme delle soluzioni di un'equazione con due variabili).

Per descrivere una funzione, invece di usare $f(x) = x^2 - 3$ possiamo anche usare l'equazione della funzione (in questo caso $y = x^2 - 3$). Per esprimere la dipendenza di $y$ dalla variabile $x$, si può anche scrivere $y(x) = x^2 - 3$.

Grafici e curve

Curve e (grafici di) funzioni sono strettamente connesse ma non sono la stessa cosa. Infatti non tutte le curve nel piano sono grafici di una funzione. Però c'è un criterio semplice per riconoscere le curve che sono grafici di una funzione:

Se una curva ha la proprietà che ad ogni ascissa corrisponde esattamente un punto sulla curva, allora essa è il grafico di una funzione, e più precisamente della funzione che assegna ad ogni numero reale $x$ la coordinata $y$ del punto (univocamente determinato) che gli corrisponde.

Se invece una curva ha la proprietà che a una ascissa corrisponde più di un punto sulla curva, allora essa non può essere il grafico di una funzione.

Esempi di grafici e curve.

Geometricamente ciò significa: una curva che interseca una retta parallela all'asse delle $y$ in più di un punto non può essere il grafico di una funzione.

Se necessario: osservare il dominio!

Per adesso abbiamo parlato solo di grafici di funzioni $\mathbb{R} \rightarrow \mathbb{R}$. Quando il dominio A di una funzione $f$ : A $\rightarrow$ B è un sottoinsieme proprio di $\mathbb{R}$ (cioè l'azione della funzione è definita soltanto per $x \in A$), il grafico è

$\{(x,f(x) | x \in A\}$ (13)

Esempio: La funzione $x \rightarrow \frac{1}{x}$ non è definita per $x = 0$. Perciò il suo grafico consiste soltanto di punti la cui coordinata $x$ è diversa da zero. È pertanto diviso in due curve separate, come vedremo più avanti.

Grafici di funzione potenza

In questo paragrafo vogliamo discutere alcuni grafici concreti. In forma modificata li ritroveremo anche nel caso di funzioni più generali. Rappresentano un elemento importante per la nostra comprensione delle funzioni.

Una funzione potenza è una funzione del tipo

$x \rightarrow x^n$ (14)

Qui $n$ (l'esponente) è un numero fisso. Considereremo in particolare i casi n = 1, 2, 3, 4, -1, -2, -3 e -4.

Si ricordi che esponenti negativi significano che viene formato anche il reciproco: $x^{-1}$ significa $\frac{1}{x}$, $x^{-2}$ significa $\frac{1}{x^2}$, ecc. Per comprendere meglio questa notazione si
veda il capitolo "Potenze".
Per $n = 1$ abbiamo $x \rightarrow x$, cioè la funzione che ad ogni $x$ assegna se stesso (la cosiddetta funzione identica).

Proprietà di una funzione

Questo paragrafo ha lo scopo di presentare concetti e metodi che servono per applicare ed analizzare le funzioni. Sono usati in molto aree della matematica moderna.

Dominio, codominio, immagine

Una funzione $f$ assegna, parlando in generale, a ciascun elemento di un insieme A un elemento (univocamente determinato) dell'insieme B. Quando si definisce una funzione, bisogna specificare anche i due insiemi A, B. C'è una certa libertà nella scelta dell'insieme B. Bisogna soltanto accertare che tutti i valori della funzione appartengano a B - in altre parole, B deve essere "grande abbastanza".
Nella massima parte dei casi che stiamo studiando A e B consistono di numeri reali, sono quindi $\mathbb{R}$ o sottoinsiemi di $\mathbb{R}$. Quindi possiamo sempre porre $B = \mathbb{R}$, poichè $f(x)$
con $x \in A$ è sempre un numero reale.

Come abbiamo visto sopra l'insieme A è detto dominio della funzione $f$.
Quando $f$ è definita da un' espressione, il dominio deve essere contenuto nell'insieme di tutti gli $x$ per i quali l'espressione è ben definita.

L'insieme B è detto codominio della funzione $f$.

L'insieme di tutti gli elementi di B che vengono assunti come valore dalla funzione, cioè che sono valore della funzione per almeno un $x \in A$, si chiama immagine della funzione $f$ e si indica con $f(A)$. Ciò sta a indicare: $\{f(x) | x \in A \}$. L'immagine coincide con il codominio B oppure ne è un sottoinsieme.

Quando una funzione è definita per $x = 0$ (cioè $0 \in A$), il punto $f(0)$ è un elemento particolare dell'immagine: esso determina l' intersezione del grafico con l'asse delle $y$ e ne è l'ordinata.

Zeri

Siano A e B sottoinsiemi di $\mathbb{R}$ e $f : A \rightarrow B$ una funzione.
Uno zero della funzione $f$ è un $x \in A$, per il quale $f(x) = 0$.

Gli zeri si trovano facilmente guardando il grafico: ad ogni coppia $(x, f(x))$ corrisponde un punto sul grafico della funzione. Se $x$ è uno zero della funzione, allora la coppia sarà del tipo $(x, 0)$. L'ordinata $y$ del punto sarà 0, e ciò significa che il punto si trova sull'asse delle $x$. Quindi gli zeri della funzione sono esattamente le ascisse delle intersezioni del grafico con l'asse delle $x$!

Connessione tra funzioni ed equazioni

Adesso un osservazione importante: se $f : A \rightarrow B$ è una funzione, l'asserzione:

$f(x)=0$ (15)

è falsa per la massima parte degli $x \in A$. Solo per certi $x \in A$ (a volte per nessuno) si verifica. In altre parole, (15) è un' equazione, e le sue soluzioni sono esattamente gli zeri della funzione $f$.
Trovare gli zeri significa risolvere un'equazione! (Vedremo più avanti alcune semplici funzioni polinomiali come esempi).

Se viceversa partiamo da un'equazione del tipo $f(x) = 0$ dove $f(x)$ è una data espressione, le sue soluzioni sono esattamente gli zeri della funzione $x \rightarrow f (x)$.

Abbiamo quindi un metodo generale per la risoluzione approssimata di un'equazione del tipo $f(x) = 0$. È molto semplice: si tracci il grafico della funzione $x \rightarrow f(x)$ e si individui (approssimativamente) la sua intersezione con l'asse delle $x$! Questo metodo si chiama risoluzione grafica di un'equazione.

Questo metodo può essere generalizzato:
un'equazione del tipo $g(x) = h(x)$ può essere scritta nella forma che abbiamo visto sopra (poichè equivalente a $g(x) - h(x) = 0$, e quindi $g(x) - h(x)$ avrà il ruolo di $f(x)$).
Oppure si tracciano i grafici di entrambi le funzioni $g$ e $h$ e si individuano i punti in cui i due grafici si intersecano. Le ascisse di questi punti di intersezione sono esattamente le soluzioni dell'equazione.

Positività

Quando la funzione $f$ è positiva in un dato $x$ (cioè $f(x) > 0$), il punto corrispondente del grafico ha ordinata positiva: il punto giace "al di sopra" dell'asse delle $x$. Se il valore della funzione è negativo, il punto corrispondente giace "al di sotto" dell'asse delle $x$.

Monotonia

Una funzione $f$ è detta:

non decrescente quando i valori non decrescono al crescere della variabile indipendente, cioè se $x_1 < x_2$ implica $f(x_1) \leq f (x_2)$

crescente quando i valori crescono al crescere della variabile indipendente, cioè se $x_1 < x_2$ implica $f(x_1) < f(x_2)$

non crescente quando i valori non crescono al crescere della variabile indipendente, cioè se $x_1 < x_2$ implica $f(x_1) \ge f(x_2)$

decrescente quando i valori decrescono al crescere della variabile indipendente, cioè se $x_1 < x_2$ implica $f(x_1) > f(x_2)$.

La funzione inversa

Sia $f: A \rightarrow B$ una funzione. Essa si dice:

iniettiva se nessun elemento dell'insieme B viene assunto più di una volta come valore, cioè se a due valori distinti di $x$ corrispondono sempre due valoridistinti della funzione (formalmente: se $x_1 \ne x_2$ implica $f(x_1) \ne f(x2))$,

suriettiva se ogni elemento di B viene assunto come valore della funzione, cioè se l'immagine coincide con l'insieme B,

biiettiva quando è iniettiva e suriettiva. In questo caso essa ci da una corrispondenza biunivoca fra gli elementi dell'insieme A e gli elementi dell'insieme B. Possiamo allora "invertire" la prescrizione e definire la cosiddetta funzione inversa $f^{-1}: B \rightarrow A$. (Attenzione: $f^{-1}(x)$ non va confunso con $f(x)^{-1} \equiv \frac{1}{f(x)}$. Per questo una funzione biiettiva è anche detta invertibile.

Esempi.

Simmetria e Antisimmetria

Una funzione $f : \mathbb{R} \rightarrow \mathbb{R}$ è detta simmetrica se per ciascun $x \in \mathbb{R}$:

$f (-x) = f (x)$ (16)

Il grafico di una funzione simmetrica è simmetrico rispetto all'asse delle $y$.

Inoltre diciamo che una funzione $f:\mathbb{R} \rightarrow \mathbb{R}$ è antisimmetrica se per ciascun $x \in R$:

$f (-x) = -f (x)$ (17)

Il grafico di una funzione antisimmetrica è simmetirco rispetto all'origine.

Esempi di funzioni simmetriche: $x^n$ per $n$ pari (cioè $1$, $x^2$, $x^4$,...), $x^2-1$, $1/{x^2}$, $1/{x^4}$, $1/{x^2-1}$, $1-{x^2}^{\frac{1}{2}}$, $\cos x$, $\sin^2 x$, $x \sin x$

Esempi di funzioni antisimmetriche: $x^n$ per $n$ dispari (cioè $x$,$x^3$,...), $x^3-3$, $ 1/x$, $1/{x^3}$, $x/{x^2-1}$, $x-{x^2}^{1/2}$, $x \cos x$, $\sin x$, $\tan x$, cot $x$

Come risulta da questi esempi, la (anti)simmetria di molte funzioni risale alla semplice identità $(-x)^2 = x^2$ che a sua volta è una conseguenza di $(-1)^2 = 1$. Perciò un'espressione in cui $x$ appare soltanto come quadrato (cioè come $x^2$) definisce sempre una funzione simmetrica. Il prodotto di due funzioni simmetriche oppure di due funzioni antisimmetriche è sempre simmetrico, mentre il prodotto di una funzione simmetrica con una antisimmetrica è antisimmetrico.

Le proprietà di simmetria di una funzione possono essere impiegate per semplificare i calcoli: se conosciamo una proprietà di una funzione (anti)simmetrica (ad esempio l'andamento del suo grafico o la posizione degli zeri) per gli $x^3<0$ avremo automaticamente anche la proprietà corrispondente per gli $x < 0$.

Esempi.

Periodicità

Si dice che una funzione $f : \mathbb{R} \rightarrow \mathbb{R}$ è periodica quando esiste un numero positivo $p$ tale che per ciascun $x \in \mathbb{R}$:

$f(x + p) = f(x)$ (18)

$p$ si chiama periodo. Al crescere di $x$ una funzione periodica "si ripete": applicando due volte (18) otteniamo $f(x + 2p) = f(x + p) = f(x)$, e più in generale si ha $f(x + np) = f(x)$ per qualsiasi numero naturale. Oltre a $p$ dunque anche tutti i suoi multipli $np$ sono periodi e perciò il grafico di una funzione periodica è caratterizzato da un motivo che continua a ripetersi.

Alcune funzioni periodiche possiedono un periodo minimo (diremo che $p$ è il periodo minimo se $p$ è un periodo, ma nessun numero $q$ tale che $0 < q < p$ è un periodo).
Esistono però anche funzioni periodiche senza periodo minimo

Esempi di funzione periodiche:

Funzione	periodo minimo
$\sin\,x$, $\cos\,x$	$2\pi$
$\tan\,x$, cot $x$, $\sin^2x$, $\cos^2x$	$\pi$
Funzione a dente di sega: nell'intervallo $-1 \le x \le 1$ si ha $f(x)=1-\mid x\mid$ e poi $f$ continua periodicamente	2

Come illustra l'ultimo esempio, la continuazione periodica ci permette di definire molte altre funzioni periodiche.

La periodicità di una funzione può essere impiegata per semplificare i calcoli: se conosciamo una proprietà di una funzione con il periodo $p$ (ad esempio l'andamento del suo grafico o la posizione degli zeri) per gli $0 \le x < p$ avremo automaticamente anche la proprietà corrispondente per gli altri $x$.

Le funzioni periodiche vengono impiegate per modellare i fenomeni oscillatori. In tal caso $x$ starà ad indicare il tempo e $p$ il periodo.

Esempi.

Grafici di funzioni polinomiali

Le funzioni date da un polinomio di grado 0,1 oppure 2 vengono utilizzate molto frequentemente.
Funzioni polinomiali fino al secondo ordine

I coefficienti del polinomio in questione sono indicati con d, k, a, b e c. Possono essere scelti a piacere. I grafici di queste funzioni sono rette oppure parabole. La loro posizione dipende dai coefficienti.

Funzioni costanti o di primo ordine...

... sono funzioni polinomiali di primo ordine o di ordine zero, cioè del tipo $x \rightarrow kx+d$, determinate da due coefficienti $k$ e $d$. Il loro grafico è sempre una retta.

Il coefficiente $d$ è il valore della funzione per $x$ uguale a 0 e indica l'ordinata del punto d'intersezione fra la retta e l'asse delle $y$. Il coefficiente $k$ misura la "pendenza" della retta e si chiama coefficiente angolare.

Ci sono vari metodi per individuare la posizione del grafico di una funzione di primo ordine. Il più semplice consiste nel trovare due punti che vi giacciono e riportarli in un sistema cartesiano. Poichè sappiamo che il grafico è una retta, la possiamo tracciare subito con un righello.

Quando $k \neq 0$, la funzione possiede esattamente uno zero. Calcolarlo significa risolvere un'equazione lineare ed è quindi un compito semplice.

Viceversa, data una retta (non parallela all'asse delle $y$) essa sarà sempre il grafico di una funzione costante (se parallela all'asse delle $x$) o di una funzione di primo grado (altrimenti).

Funzioni di secondo ordine (quadratiche)...

... sono funzioni polinomiali di secondo ordine, cioè del tipo $x \rightarrow a x^2 + bx + c$ (con $a \neq 0$), determinate da tre coefficienti a, b e c. Il loro grafico è una parabola.

Abbiamo già visto esempi di funzioni di secondo ordine in questo capitolo. La "funzione quadrato" $x\rightarrow x^2$ all'(inizio) del capitolo e la funzione $x \rightarrow x^2 - 3$ quando abbiamo introdotto il concetto di grafico di una funzione.

La posizione del grafico di una funzione di secondo ordine può essere individuata attraverso un'analisi dell'espressione quadratica che la definisce. Il segno di $a$ ci dice se la parabola volge la sua concavità verso l'alto o verso il basso. Il valore assoluto di a determina la forma della parabola: quando $\mid a\mid < 1$ essa sarà più "aperta", quando $\mid a\mid > 1$ essa sarà più "chiusa" rispetto alla "parabola normale" (quella per $a = 1$).

Abbiamo già studiato le espressioni quadratiche in un altro capitolo. Alcune delle loro proprietà adesso assumono un significato geometrico.

Una funzione di secondo ordine può avere due, uno oppure nessuno zero, poichè una parabola - a seconda della sua posizione - può intersecare l'asse delle $x$ in due, uno oppure in nessun punto. Questo è il fondamento geometrico del fatto che un'equazione di secondo grado può avere due, una oppure nessuna soluzione!

Il concetto di funzione ci aiuta dunque a capire meglio le espressioni e le equazioni quadratiche.

Esempio: gli zeri della funzione $x \rightarrow x^2 -3$ discussa sopra sono le soluzioni dell'equazione $x^2 - 3=0$, cioè $x= \pm \sqrt{3} \approx \pm 1.732$. Queste sono esattamente le ascisse dei punti di intersezione fra l'asse delle $x$ e il grafico riportato sopra.

Possiamo anche capovolgere il ragionamento: per risolvere l'equazione $x^2 - 3 =0$ dobbiamo considerare il grafico riportato sopra della funzione $x \rightarrow x^2 -3$. Esso ci informa sul numero e il valore (approssimato) delle soluzioni. Si tratta di un caso particolare del metodo generale di risoluzione grafica di un'equazione che avevamo discusso sopra.

Esempi.