ESPONENZIALI E LOGARITMI
Potenze con esponente reale
In questo capitolo hanno un ruolo fondamentale le potenze i cui esponenti sono numeri reali arbitrari. Vogliamo dunque innanzitutto discutere che cosa intendiamo quando parliamo di tali potenze.
Una potenza è un'espressione di forma $a^x$ in cui a è detta base e x esponente. Usiamo il carattere x per indicare l'esponente, visto che in questo capitolo ci interessa studiare come una potenza dipende dal suo esponente. Abbiamo già visto prima come definire una potenza con base positiva $(a > 0)$ e esponente razionale x, e ci ricordiamo la regola (identità)
| $${a^{x+y} = a^{x} \cdot a^y}$$ | (1) |
che vale per tutti i numeri razionali x,y. L'abbiamo già usata prima come guida preziosa e continuerà ad avere un ruolo fondamentale.
Vedi anche la lezione: Potenze con esponenti razionali
Vogliamo chiederci adesso
se è possibile definire una potenza anche quando l'esponente è un numero reale arbitrario (quindi anche
per esponenti irrazionali che non possono essere
scritti come quoziente di due numeri interi, come ad esempio
${ \sqrt{2}}$ o ${\pi}$). Ha un senso formare la potenza $2^{\pi}$? Vedremo tra breve che ciò è
veramente possibile. A tal fine adopereremo
il fatto che ciascun numero irrazionale può essere approssimato da numeri razionali con precisione arbitrariamente grande.
Se come esponente
vogliamo scegliere ad esempio ${\pi}$, consideriamo la successione di numeri
e ad ogni passo successivo aggiungiamo la cifra successiva nella rappresentazione decimale di ${\pi}$. Questi numeri si avvicinano sempre più a ${\pi}$ (più precisamente: si avvicinano a piacere a ${\pi}$ ), e sono tutti razionali (ad esempio ${3.14=\frac{314}{100}}$ è quoziente di due numeri interi), quindi possono essere scelti come esponenti di una potenza. Consideriamo adesso le potenze che possiamo formare con questi numeri:
Per spiegare con un esempio che cosa avviene, poniamo a=2 e guardiamo le rappresentazioni decimali delle prime sei potenze:
| $x$ | ${2^x}$ |
| 3.14 | 8.815240927... |
| 3.141 | 8.821353304... |
| 3.1415 | 8.824411082.. |
| 3.14159 | 8.824961595... |
| 3.141592 | 8.824973829... |
| 3.1415926 | 8.824977499... |
Vediamo che i numeri nella colonna di destra variano sempre meno. Essi tendono a un certo numero reale, questo numero si indica con ${2^\pi}$. La sua rappresentazione decimale inizia così 8.824977827... e in linguaggio matematico si chiama "limite" della successione numerica riportata nella colonna di destra. Lo stesso metodo può essere usato anche per altre basi (positive) a e per altri esponenti (irrazionali) $x$. Poichè la regola (1) vale per gli esponenti razionali con i quali approssimiamo a piacere gli esponenti irrazionali, concludiamo che essa vale anche per questi ultimi.
Riassumiamo:
Se ${a>0}$, la potenza ${a^{x}}$ può essere definita per esponenti reali arbitrari x. La regola (1) è ancora
valida: adesso x e y
sono numeri reali arbitrari.
Per questo concetto più generale di potenza valgono - oltre alla (1) - anche le altre regole che
abbiamo già visto per esponenti razionali.
Regole per il calcolo con le potenze .
Funzioni esponenziali
Visto che adesso possiamo usare qualsiasi numero reale come esponente, possiamo chiederci come la potenza di una data base (positiva) a dipende dal suo esponente. In altre parole, possiamo assegnare
| $$x\rightarrow a^{x}$$ | (2) |
Ciò definisce una funzione sull'insieme dei numeri reali. Tale funzione si chiama funzione esponenziale. Anche per funzioni più generali del tipo
| $$x\rightarrow c \cdot a^{bx}$$ | (3) |
dove b e c sono numeri costanti, si usa lo stesso nome.
Le funzioni esponenziali hanno un ruolo fondamentale in matematica e in molte applicazioni. Servono a comprendere i sistemi dinamici, siano essi di natura fisica, chimica, biologica o economica. Vedremo come vengono impiegate per modellare processi di crescita o di decadimento. Ma le ritroviamo anche in molti altri contesti, a partire dalla teoria delle probabilità fino alla fisica quantistica. La teoria delle equazioni differenziali non sarebbe concepibile senza le funzioni esponenziali e la loro generalizzazione all'ambito dei numeri complessi; mostra inoltre una relazione profonda con la trigonometria e i processi oscillatori, le cui applicazioni giungono fino alla tecnica delle correnti alternate.
La vasta applicabilità delle funzioni
esponenziali deriva dalla semplicità dell'idea che ne sta alla base. Riguardiamo per un attimo la loro
"genesi":
siamo partiti da una semplice notazione ($a^{n}$ come prodotto n-uplo di a con se stesso) e l'abbiamo estesa successivamente a situazioni
sempre più generali,
ammettendo come esponenti prima i numeri interi, poi i razionali e infine i reali. Le prime due generalizzazioni
(discusse in un capitolo precedente) si basano
sostanzialmente sul principio di mantenere valida la regola (1).
L'ampliamento ai numeri reali risulta poi quasi automaticamente.
Batteri e crescita esponenziale
Illustreremo adesso il ruolo delle funzioni esponenziali nei modelli matematici che descrivono processi di crescita. Consideriamo una colonia di batteri. Assumiamo che la sua crescita (determinata da divisioni di cellule) sia caratterizzata dalle seguenti tre proprietà:
- In intervalli temporali di uguale lunghezza il numero di batteri aumenta di uguale fattore.
- All'inizio la colonia è composta da 1000 batteri.
- Dopo un'ora il numero di batteri è raddoppiato.
Cominciamo con alcune osservazioni su queste proprietà:
- La prima proprietà è quella decisiva, poichè caratterizza la natura del processo: si basa sull'ipotesi che ogni batterio si riproduca con fattore costante, indipendentemente dalla grandezza della colonia e dal tempo trascorso. La parola essenziale è "fattore": la colonia non aumenta di un numero fisso di batteri per unità di tempo, bensì di un numero che è proporzionale alla grandezza raggiunta dalla colonia. Più batteri abbiamo, più ne aggiungeremo, e questo si svolge in maniera continua. Un processo del genere si chiama - per motivi che comprenderemo subito - crescita esponenziale.
- Le proprietà (2) e (3) forniscono i dati quantitativi caratteristici del processo (il valore iniziale e il fattore di crescita). Ci servono per poter fare previsioni concrete (quantitative).
- Le tre ipotesi (in particolare la proprietà 1) forniscono naturalmente solo un modello:
- In realtà il numero di batteri è discreto, cioè non aumenta in maniera continua, bensì in maniera saltuaria, solo in determinati momenti: dopo un secondo può non essere cambiato nulla, mentre nel secondo successivo può aggiungersi un nuovo batterio. (Inoltre si potrebbe obiettare che non è affatto chiaro a partire da quando si può parlare di un "nuovo batterio", visto che ogni divisione di cellule necessita di un lasso di tempo). Per una colonia grande però possiamo trascurare questi problemi e trattare sia il "numero di batteri" sia il tempo trascorso come grandezze continue descritte da numeri reali.
- Non vogliamo entrare nel merito su quanto la legge di crescita dei batteri si avvicini alla realtà.
- La crescita esponenziale non dura in eterno. Prima o poi si raggiungono limiti che rallentano il processo e che allo stesso tempo determinano i limiti del modello.
- Nonostante queste possibili obiezioni, è importante studiare un modello dal punto di vista matematico e individuare le previsioni che esso fornisce. I limiti del campo di validità del modello si scoprono spesso solo dopo una tale analisi. Non discuteremo dunque ulteriormente l'applicabilità del modello, ma metteremo il modello stesso al centro delle nostre considerazioni.
Iniziamo con l'analisi del modello definito dalle tre proprietà sopra descritte. Il nostro scopo è prevedere la grandezza della colonia dopo un certo lasso di tempo $t$. Per la terza proprietà è facile calcolare il numero di batteri per ogni ora intera: dopo 1 ora ci sono 2000 batteri, dopo 2 ore ci sono 4000 batteri, dopo 3 ore ci sono 8000 batteri, ecc. Soffermiamoci un momento e riflettiamo su come si ottengono questi numeri:
- All'inizio (ora 0) ci sono ${1000 =1000 \cdot 2^{0}}$.
- Dopo 1 ora il numero di batteri è raddoppiato, quindi ${1000 \cdot 2 = 1000 \cdot 2^{1}}$ batteri.
- Dopo 2 ore il loro numero è aumentato nuovamente di fattore 2, cioè ci sono ${1000 \cdot 2 \cdot 2 =1000 \cdot 2^{2}}$ batteri
- Dopo 3 ore ci sono ${1000 \cdot 2^{2} \cdot 2 =1000 \cdot 2^{3}}$ batteri.
Continuiamo a piacere con questo ragionamento e vediamo che: dopo t ore la colonia consiste di
| $1000 \cdot 2^{t}$ batteri | (4) |
Questa formula è estremamente comoda. Se vogliamo determinare la grandezza della colonia dopo 24 ore, invece di raddoppiare il numero
per 24 volte, basterà
calcolare il numero ${1000 \cdot 2^24}$. Otterremo 16777216000, cioè (arrotondato) 16.8 miliardi di batteri, un numero
enorme. Adesso capiamo la ragione per il
nome "esponenziale": la varibile del tempo $t$ (il numero di ore trascorse) compare
come esponente nella formula (4).
Quando aumenta $t$ il valore ${2^{t}}$ cresce esponenzialmente e raggiunge
presto valori enormi.
In questo capitolo troveremo spesso calcoli simili.
Per poterli svolgere agevolmente, mettiamo qui a disposizione un calcolatore di crescita:
Calcolatore di crescita
Dati tre numeri a, b, c verrà calcolato $a \cdot b^{c}$. Per il calcolo di cui sopra inserire 1000 nella prima casella, 2 nella seconda
casella e 24 nella terza
casella (elevare) e cliccare sul segno uguale.
(Qualsiasi altro calcolatore elettronico può servire allo stesso scopo naturalmente).
La nostra formula
(4) può dare l'impressione di aver già trovato un modello matematico che descrive la crescita della
colonia di batteri in maniera soddisfacente.
Nel diagramma qui sotto vediamo che cosa ci fornisce: il numero di batteri in un determinato
momento è riportato verticalmente sopra il punto corrispondente nell'asse
del tempo. Quando inseriamo successivamente t=1, t=2, t=3 ecc.
la nostra formula (4) ci fornisce i punti gialli: il numero di batteri presenti
ad ogni ora intera. Ma poniamoci una
domanda innocente, e come spesso in matematica, con una piccola domanda mettiamo in movimento grandi cose: quanti batteri ci
sono dopo
mezz'ora? Dove si trova esattamente il punto nel nostro diagramma che corrisponde a ${\frac{1}{2}}$ sull'asse del tempo?
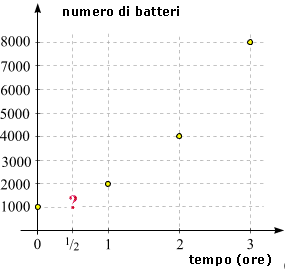
Per rispondere a questa domanda, ci serve la proprietà (1) del nostro sistema: "In intervalli temporali di uguale lunghezza il numero di batteri aumenta di uguale fattore". Questo risolve il problema: dopo mezz'ora i batteri saranno aumentati di un fattore che per adesso non conosciamo e che indichiamo con q. Dopo $\frac{1}{2}$ ora dall'inizio ci sono dunque ${1000\ q}$ batteri. Nella mezz'ora successiva si riproducono - secondo la proprietà (1) - nuovamente con il fattore di crescita q, quindi adesso avremo ${1000\ q^2}$ batteri. D'altra parte sappiamo però che in totale è trascorsa 1 ora, per cui per la proprietà (3) il numero dei batteri deve essere raddoppiato. Deduciamo che ${q^2 = 2}$, da cui segue ${q = \sqrt{2} = 1.414213562...}$. La risposta alla nostra domanda è dunque che dopo mezz'ora ci sono (circa) 1414 batteri. Il numero esatto, previsto dal nostro modello, è ${1000 \sqrt{2}}$. Osserviamo adesso che ciò può anche essere scritto come $1000 \cdot 2 \cdot \frac{1}{2}$, in quanto $2\cdot\frac{1}{2}$ è proprio la radice quadrata di 2. Ma allora la formula (4) vale anche per $t=\frac{1}{2}$!
Veramente non si tratta di una scoperta sorprendente! Per adesso avevamo definito potenze con esponenti razionali senza riferimento ad applicazioni concrete, ma soltanto per motivi formali - guidati soprattutto dall'intenzione di mantenere valida la regola (1) anche per esponenti razionali - non pensavamo affatto a batteri e processi di crescita. Eppure adesso scopriamo che la convenzione di scrivere la radice quadrata di $a$ come ${ a^{\frac{1}{2}}}$ si confà alla descrizione della crescita di batteri. Anche il nostro calcolatore di crescita naturalmente conosce la convenzione - si provi a inserire $\frac{1}{2}$ oppure 0.5 nella casella per l'esponente!
Ma non abbiamo ancora finito: non è difficile dimostrare che la formula (4) può essere applicata a qualsiasi lasso di tempo reale (positivo) $t$. In altre parole:
| La crescita della colonia di batteri è descritta dalla funzione esponenziale ${ t\rightarrow1000 \cdot 2t}$ cioè dalla formula (4), in cui adesso possiamo inserire numeri reali (positivi) arbitrari t! | (5) |
Per dimostrare quest'asserzione basta generalizzare l'argomento di prima da ${t = \frac{1}{2}}$ a un t razionale qualsiasi e poi estendere
al caso dove t è un
numero reale. Torneremo più avanti sul perchè le funzioni esponenziali sono adatte a descrivere processi esponenziali
e ne capiremo meglio la ragione profonda -
connessa alla regola (1).
Poichè t adesso può essere un punto qualsiasi sul ramo positivo della retta dei numeri, possiamo migliorare la
rappresentazione grafica del
processo: la linea rossa nel diagramma qui sotto rappresenta il grafico della funzione esponenziale (5).
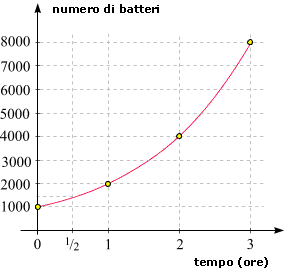
Adesso possiamo risolvere semplici problemi del tipo: qual è il numero di batteri dopo un'ora e un quarto?
Soluzione: un'ora e un quarto è pari
a 1.25 ore. Inseriamo t= 1.25 in (4) e otteniamo (con l'ausilio del
calcolatore di crescita) 2378.41423...,
arrotondando: 2378 batteri.
Altri processi di crescita esponeziale
Molti sistemi si comportano in maniera simile ai nostri batteri visti sopra. Qui vogliamo citarne alcuni e mostrare come possono essere
interpretati
matematicamente.
Due esempi:
- Ancora batteri:
- Caratterizzazione del processo: l'area occupata da una colonia di batteri cresce esponenzialmente ed è inizialmente pari a 20 cm2. Ogni minuto aumenta del 4%
- Individuazione della funzione esponenziale: ciò significa che dopo un minuto ha raggiunto il 104% della grandezza iniziale, cioè cresce con il fattore 1.04. Con lo stesso ragionamento usato nell'esempio discusso sopra dopo t minuti l'area è pari a ${20\cdot 1.04^{t}}$ cm2. (Si verifichi inserendo t=1: dopo un minuto si prevede un'area di ${20\cdot 1.04}$ cm2 che corrisponde ai dati)
- Ninfee in uno stagno:
- Caratterizzazione del processo: le ninfee sulla superficie di uno stagno si riproducono esponenzialmente. All'inizio ce ne sono 17. Il loro numero raddoppia ogni 4 giorni.
- Individuazione della funzione esponenziale: dopo x periodi di 4 giorni il loro numero è pari a $17 \cdot 2^x$. Poichè sono trascorsi in tutto $t=4x$ giorni, il numero delle ninfee dopo $t$ giorni è dato da ${17 \cdot 2^\frac{t}{4}}$. (Si verifichi inserendo t=4: dopo 4 giorni si prevede il numero $17 \cdot 2$ che corrisponde ai dati).
Decadimento radioattivo e decadimento esponenziale
Non solo la crescita, anche la diminuzione di una grandezza può avvenire in maniera esponenziale. Per descrivere tali processi basterà modificare leggermente le nostre considerazioni. Pensiamo a una sostanza radioattiva, cioè una sostanza nella quale si trova un certo numero di nuclei atomici "disintegrabili". Prima o poi ognuno di questi nuclei si "disintegrerà", cioè libererà una particella elementare (emettendo radiazioni) e si trasformerà in un nucleo di tipo stabile. Più nuclei "disintegrabili" si trovano nella sostanza, più forte è la radiazione emessa. Poichè i nuclei "disintegrabili" vanno man mano esaurendosi, la radiazione emessa diminuirà con il passare del tempo. Assumiamo che la radiazione emessa dalla nostra sostanza sia caratterizzata dalle seguenti tre proprietà:
- In intervalli temporali di uguale lunghezza la sua intensità diminuisce di uguale fattore.
- All'inizio è pari a 1000 (in un'unità di misura di cui adesso non vogliamo discutere).
- Dopo ogni ora il suo valore è dimezzato.
Queste proprietà sono quasi identiche a quelle viste sopra per la crescita della colonia di batteri. L'unica differenza è che dopo un'ora la grandezza che ci interessa non vale 2 volte, bensì $\frac{1}{2}$ volta, cioè $2^{-1}$ volte il valore iniziale. Possiamo quindi ripetere tutti i ragionamenti del paragrafo precedente e dobbiamo soltanto ricordare che il "fattore" di cui si parla nella proprietà 1 adesso è minore di 1. Con una discussione analoga a quella per la formula (4) si deduce che l'intensità dopo t ore è scesa al valore
| ${1000 \cdot (\frac{1}{2})^{t}}$ batteri | (6) |
Questo può essere anche espresso come $1000 \cdot (2^{-1})^{t}$ e poichè $(2^{-1})^{t} = 2^{-t}$ possiamo sostituire la (6) con
| $$1000 \cdot 2^{-t}$$ | (7) |
Scegliere (6) oppure (7) non cambia minimamente la descrizione del processo. Spesso si preferisce la seconda versione (7) in quanto il segno negativo nell'esponente ci mostra subito che si tratta di un processo di decadimento e non di crescita. Come nel paragrafo precedente si vede che queste due formule sono applicabili a qualsiasi t reale (positivo). Il nostro calcolatore di crescita può essere usato (malgrado il nome) anche per processi di decadimento. Si provi a calcolare l'intensità di radiazione dopo un'ora e un quarto (1.25 ore)!
Un processo di questo tipo si chiama decadimento esponenziale. Il tempo necessario per ridurre la grandezza osservata alla metà del suo valore iniziale (nel nostro esempio: 1 ora) si chiama tempo di dimezzamento.
Ovviamente anche in questo caso le nostre ipotesi iniziali (le tre proprietà viste sopra) ci forniscono soltanto un modello. Quando cresce t il valore $2^{-t}$ cala "esponenzialmente" e raggiunge presto valori piccolissimi. Ma quando non ci sono più nuclei disintegrabili, o eventualmente anche prima, si raggiunge il limite del modello.
Confrontando questi esempi con quelli del paragrafo precedente vediamo che i processi di crescita o decadimento esponenziale sono descritti dal medesimo formalismo: quello della funzione esponenziale, le cui proprietà saranno oggetto del prossimo paragrafo.
Esempi di crescita esponenziale.
Proprietà della funzione esponenziale
Come abbiamo visto nei due paragrafi precedenti attraverso diversi esempi, un processo esponenziale è dato da una funzione esponenziale, cioè una funzione del tipo (3).La scriviamo così
| $$f(x) = c \cdot a^{bx}$$ | (8) |
In tutti gli esempi considerati le funzioni di crescita o decadimento hanno questa forma. Differiscono soltanto nei valori diversi per le costanti ${a(>0)}$, b e c (anche dette parametri). In seguito discuteremo alcune proprietà essenziali di queste funzioni.
Perchè le funzioni esponenziali sono adatte a descrivere processi esponenziali
È istruttivo soffermarsi un attimo su che cosa rende così speciali le funzioni di forma (8). Abbiamo caratterizzato i processi di crescita e decadimento attraverso il fatto che la grandezza osservata "aumenta (oppure cala) di uguale fattore in intervalli di uguale lunghezza", anche se non si tratta sempre di processi temporali, ma soltanto del variare di una grandezza in dipendenza dall'altra (come ad esempio l'intensità di un raggio luminoso in funzione dello spessore della lastra di vetro attraverso cui passa). Questa proprietà decisiva si ritrova nelle funzioni di tipo (8) nella forma seguente:
|
In intervalli di uguale lunghezza il valore della funzione varia di uguale fattore. Più concretamente ciò significa: se x aumenta di un certo valore s e diventa $x+s$ allora la variazione corrispondente nel valore della funzione (da ${f(x)}$ a $f(x + s)$) è del tipo $f(x + s) =$ fattore che dipende solo da $s \cdot f(x)$ |
Ciò si dimostra facilmente inserendo ${x + s}$ a posto di x nella (8):
| $$f(x + s) = c a^{b(x + s)} = c \cdot a^{bs} \cdot a^{bx} = a^{bs} f(x)$$ | (9) |
La seconda uguaglianza segue da (1), la regola di calcolo fondamentale per le potenze, per la terza uguaglianza abbiamo impiegato (8). Questa identità vale per qualsiasi numero reale $s$, non solo per quelli positivi. Con ciò abbiamo anche dimostrato: il "fattore che dipende solo da $s$", è ${a^{bs}}$. Si noti che non dipende da x. Scegliendo un x a piacere. Quando x aumenta (additivamente) di $s$, il valore della funzione varia (moltiplicativamente) del fattore ${a^{bs}}$.
Questo intreccio di addizione e moltiplicazione deriva dalle proprietà delle potenze: la connessione fra il prodotto (di potenze) e la somma (degli esponenti) espressa in (1). Vediamo dunque che l'identità (1) è la ragione profonda del fatto che le funzioni esponenziali sono adatte a descrivere processi esponenziali.
Dominio
Le funzioni esponenziali sono definite su tutti i numeri reali x, quindi il loro dominio è l'insieme $\mathbb{R}$. Per modellare un processo esponenziale si utilizza spesso solo una parte del dominio (in genere $x\ge0$) poichè ogni processo realistico possiede un punto di partenza.
Monotonia e iniettività
Vogliamo chiudere questo paragrafo con alcune proprietà importanti della funzione esponenziale. Consideriamo funzioni del tipo (8) con ${c>0}$. Esse sono tutte positive: $f(x) >0$ per ogni $x\in\mathbb{R}$. Con l'abbreviazione $A = a^b$ abbiamo:
- Se $A>1$, allora f è una funzione crescente:
quindi descrive un processo di crescita.$x_{1} < x_{2}$ implica $f(x_{1}) < f(x_{2})$ (10) - Se $A<1$, allora f è una funzione decrescente:
quindi descrive un processo di decadimento.$x_{1} < x_{2}$ implica $f(x_{1}) > f(x_{2})$ (11) - Nel caso limite A=1, che si verifica solo quando a=1 oppure b=0, f è una funzione costante.
Dimostrazione: È una conseguenza immediata di (9) sostituendo ${a^{bs}}$ con ${A^{s}}$: Per ${s>0}$ possiamo porre $x_{1} \equiv x$ e $x_{2} \equiv x+s$ e concludere ${f(x_{2}) = A^s f(x_{1})}$.
A seconda che $A$ (e perciò anche ${A^s}$) sia maggiore o minore di 1, otteniamo che ${f(x_{2})}$ è maggiore o minore di ${f(x_{1})}$.
La monotonia implica che le funzioni considerate (per ${c>0}$ e ${A\ne 1}$) sono iniettive . Ciò significa che non possono assumere lo stesso valore più di una volta.
Dimostrazione: Se ${x_{1}\ne x_{2}}$ si ha ${x_{1} > x_{2}}$ oppure ${x_1 < x_{2}}$, e per (10) e (11) segue che ${f(x_{1})}$ è maggiore oppure minore di ${f(x_{2})}$. Quindi due valori ${f(x_{1})}$ e ${f(x_{2})}$ possono solo coincidere quando ${x_{1} = x_{2}}$.
L'ultima proprietà che menzioniamo è il fatto che ognuna delle funzioni considerate (per ${c>0}$ e ${A\ne 1}$) può assumere qualsiasi valore positivo. In altre parole la sua immagine è l'insieme ${\mathbb{R}^{+}}$: i loro grafici si avvicinano a piacere all'asse delle ascisse $x$ nella parte positiva oppure negativa (a seconda che ${A < 1}$ oppure ${A > 1}$) e tendono a infinito dall'altra parte. Quindi ogni numero positivo, per grande o piccolo che sia, viene assunto come valore della funzione. Insieme all'iniettività ciò significa che ogni numero positivo viene assunto come valore esattamente una volta.
Per capire meglio queste proprietà si consiglia di studiare alcuni di questi grafici, ad esempio per le funzioni $x \rightarrow \left(\frac{1}{2}^{x}\right)$ e $ x \rightarrow 2^{x}$.
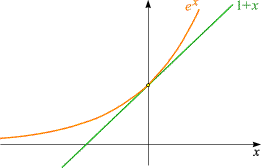
Il numero di Eulero $e$
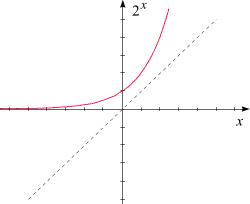
Il numero $e$ fu scoperto nel diciottesimo secolo dal matematico svizzero Leonardo Eulero. Come ${\pi}$ si tratta di un numero irrazionale, e la sua rappresentazione decimale inizia così
| e = 2.71828182845904523536028747135266... | (12) |
Ecco una definizione concisa di: $e$ è l'unico numero positivo per il quale
| ${e^{x}\ge (1 + x)}$ per ogni ${x\in \mathbb{R}}$ | (13) |
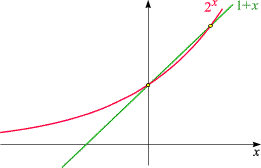
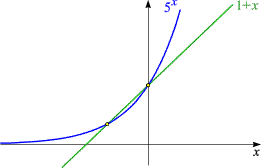
Nel riquadro qui sopra troviamo i grafici di queste due funzioni: quello di $e^x$ giace - a parte il punto (0, 1) - completamente "sopra" la retta che forma il grafico di $1+ x$. La base $e$ è l'unica ad avere questa proprietà: se $a\ne e$, il grafico di $a^x$ interseca la retta in due punti e ne giace quindi parzialmente "al di sotto". Confrontiamo con $2^x$ e $5^x$:
Come mai diamo tanta importanza alla proprietà (13)? Ciò ha a che fare con l'andamento per piccoli $x$ delle funzioni esponenziali di tipo (2), cioè le funzioni ${x\rightarrow a^x}$. Dai grafici precedenti si vede che le funzioni ${e^x}$ e ${1+x}$ hanno un andamento molto simile intorno al punto ${(0,1)}$, cioè che
| ${e^z \approx 1+x}$ per ${\mid x \mid \ll 1}$ | (14) |
Ciò sta a indicare che per piccoli $x$ la differenza fra le due espressioni ${e^x}$ e ${1+x}$ è un numero di ordine di grandezza molto
inferiore a $x$.
Verifichiamolo numericamente per $x=0.01$: con il valore (12) calcoliamo ${e^{0.01}=1.01005016...}$,
la cui differenza da ${1+0.01}$
è soltanto 0.00005016... un numero notevolmente più piccolo di 0.01! Quanto più piccolo sarà $x$, tanto
migliore sarà l'approssimazione (14).
Per altre basi non vale questo discorso: se ${a\ne e}$, allora per piccoli
$x$ abbiamo l'approssimazione ${a^x \approx 1 + c^x}$, dove c è una costante ${\ne 1}$
(il cui valore dipende da $a$).
La definizione (13) ci permette anche di calcolare $e$.
Consideriamo l'espressione
| $${\left(1+\frac{1}{n}\right)^n}$$ | (15) |
e pensiamo di scegliere per $n$ successivamente tutti i numeri naturali. Per n = 1 otteniamo il valore 2, per n=2 otteniamo 2.25 ecc.
Passiamo a numeri più grandi:
per n = 10 otteniamo 2.5937424601, per n = 100 otteniamo 2.7048138294..., e per n = 1000 otteniamo
2.7169239322... Vediamo che questi numeri si avvicinano sempre
più a (12). Per n = 10000 otteniamo 2.7181459268...,
la cui differenza da (12) è già inferiore a un centesimo per cento.
Infatti $e$ è il numero cui tende
(15) quando $n$ cresce a piacere.
Nel linguaggio matematico si dice che $e$ è il "limite" della successione definita da (15). Ciò ci
permette di calcolare
numericamente $e$ (con precisione grande a piacere). In molti libri il numero $e$ viene definito così. Ci sono
però anche altri metodi - più efficaci -
per calcolare numericamente $e$ (e anche le grandezze connesse ${e^x}$ per un dato $x$).
$e$ come base naturale
Dal punto di vista dell'andamento per piccoli $x$ abbiamo visto che $e$ ha un ruolo speciale fra le varie basi di potenze. Per questo viene anche chiamata base naturale. La funzione ${x\rightarrow e^x}$ è così importante che si usa un simbolo apposito per indicarla. Si indica con exp scrivendo
| $${exp(x) = e^x}$$ | (16) |
Questa notazione è particolarmente utile quando invece di x si ha un'espressione complicata. Quando si parla della funzione esponenziale,
generalmente si
intende questa funzione. Potete usare il calcolatore di crescita per trovare le
potenze della base naturale, inserendo
il numero 1 nella prima casella e la lettera E - che sta a indicare e - nella seconda casella.
In molte applicazioni, quando si usano le funzioni esponenziali,
si sceglie di lavorare con la base $e$. In particolare i processi
di decadimento (ad esempio la decadimento radioattiva) studiati in fisica vengono
espressi in forma
| $$f(t)=f(0)\, e^{-\lambda\, t}$$ | (17) |
dove $f$ è la grandezza studiata (ad es. l'intensità di radiazione), $t$ rappresenta il tempo e ${\lambda}$ si chiama costante di decadimento. Vedremo più sotto come la costante radioattiva è legata al tempo di dimezzamento. Analogamente i processi di crescita vengono spesso espressi in forma ${f(t)=f(0)\ e^{\lambda t}}$ dove ${\lambda}$ si chiama fattore di crescita.
Logaritmi
Scegliamo una base ${a>0 (a\ne 0)}$ e consideriamo la funzione esponenziale ${x\rightarrow a^x}$ definita da (2). Come abbiamo visto sopra ogni numero positivo viene assunto esattamente una volta come valore della funzione. Nel linguaggio matematico ciò si esprime così: dato un numero positivo $b$ esiste uno e un solo numero reale $x$ con
| $$a^x=b$$ | (18) |
In altre parole: l'equazione (18) ha una e una sola soluzione per x.
Esempi: l'equazione ${3^x=9}$ ha (l'unica) soluzione
${x=2}$. L'equazione ${16^x = 4}$ ha (l'unica) soluzione ${x=\frac{1}{2}}$.
L'equazione ${(\frac{1}{2})^{x}=8}$ ha (l'unica) soluzione x=-3.
Ma qual è (l'unica) soluzione dell'equazione ${3^x=8}$? Sarà un
numero un po' più piccolo di 2, ma possiamo determinarlo con precisione? Purtroppo le operazioni
che conosciamo per adesso non ci aiutano a
risolvere il problema! La soluzione cercata è un numero irrazionale che non può essere espresso come frazione, radice
o simili. Possiamo
trovare delle approssimazioni per calcolarla numericamente. Per il momento però è più importante trovare un concetto matematico preciso.
Cominciamo col darle un nome: si chiama il "logaritmo di 8 in base 3". In generale diremo:
| Definizione: Dati ${a>0\ (a\ne 1)}$ e ${b>0}$, chiamiamo logaritmo di $b$ in base $a$ il numero (univocamente
determinato) $x$ per il quale si ha ${a^x=b}$, cioè la soluzione dell'equazione (18). Lo indichiamo con il simbolo
${log_a}$ e scriviamo $x$ come ${log_a\,b}$ oppure in parentesi ${log_a(b)}$: Da ${a^x=b}$ segue ${x=log_a\, b}$. |
(19) |
Nota bene:Il calcolo numerico dei logaritmo sarà delegato a calcolatori tascabili o computer. Qui mettiamo a disposizione un calcolatore di Log:
Calcolare il logaritmo
Si provi a calcolare le soluzioni delle equazioni menzionate sopra: ${log_3\, 9, log_{16}\,4, log_{\frac{1}{2}}\,8\,e\, log_3\,8}$. Quest'ultima risponde alla nostra domanda riguardo alla soluzione dell'equazione ${3^x=8}$. Come ci dobbiamo immaginare il logaritmo? Si tratta dell'inverso dell'elevazione a potenza. Calcolare ${log_a\,b}$ risponde alla domanda: con quale esponente si può rappresentare $b$ come potenza di $a$, cioè per quale x si ha ${b=a^x}$? In parole povere: quante volte dobbiamo moltiplicare la base $a$ "con se stessa" per ottenere $b$?
Guardiamo ad esempio la base 10 che ci fornisce la rappresentazione decimale dei numeri reali: abbiamo ${log_{10}\,1000=3}$, poichè 1000 può essere scritto come ${10^3}$. Dunque ${log_{10} 1000}$ è il numero degli zeri che si trovano nella rappresentazione decimale di 1000, cioè 3. Che ${log_{10}\,0.01=-2}$ deriva dal fatto che il numero 0.01 scritto come "potenza di dieci" è uguale a ${10^{-2}}$. La relazione ${log_{10}\,1500=3.17609...}$ deriva dal fatto che il numero 1500 scritto come "potenza di dieci" è uguale a ${10^{3.17609...}}$. Per questa proprietà, di fornire l'esponente della rappresentazione come potenza di dieci, il logaritmo in base 10 è adatto a indicare grandi numeri. Ad esempio, per un numero la cui rappresentazione decimale possiede 54 cifre prima della virgola (e che quindi è molto grande), esso sarà compreso fra 53 e 54. Qui ci si basa sull'idea di utilizzare il "numero di cifre" come misura della grandezza di un numero. Questo approccio è molto utile quando in un problema compaiono numeri di ordine di grandezza diversa.
Funzioni logaritmiche
Possiamo considerare il logaritmo anche in questi termini: la funzione esponenziale ${ x\rightarrow a^x}$ con ${(a\ne 1)}$ ha, come abbiamo visto sopra, la proprietà di assumere esattamente una volta ogni numero positivo come valore. In altre parole, essa ci dà una corrispondenza biunivoca fra l'insieme ${\mathbb{R}}$ di tutti i numeri reali e l'insieme ${\mathbb{R}^+}$ dei numeri reali positivi. Si tratta quindi di una funzione invertibile ${\mathbb{R}\rightarrow \mathbb{R}^+}$.
La funzione logaritmo ${b\rightarrow log_a\,b}$ non è altro che la sua funzione inversa .
Questa caratterizzazione ci dice immediatamente come trovare il grafico della funzione logaritmo in base $a$ partendo da quello della funzione esponenziale corrispondente: se nell'equazione (18) consideriamo il numero $b$ in dipendenza di $x$ possiamo scrivere la funzione esponenziale come ${b\equiv b(x)=a^x}$.
Adesso pensiamo di risolvere questa "equazione" in x: la soluzione (univoca) x dipende dal numero $b$ per cui la funzione
logaritmo può essere
espressa in forma ${x\equiv x(b)=log_a\,b}$. Queste due equazioni descrivono la medesima relazione fra le grandezze
x e $b$ data dall'equazione
(18), solo che una volta la variabile indipendente è x e l'altra volta è $b$. Il grafico
della funzione esponenziale viene raffigurato
in un sistema cartesiano dove l'asse delle x è orizzontale e quella di $b$ è verticale, il
grafico della funzione logaritmo invece in un sistema cartesiano
dove l'asse di $b$ è orizzontale e l'asse delle x è verticale.
La differenza fra i due sistemi cartesiani consiste soltanto nel fatto che la notazione
degli assi è scambiata. Poichè i due grafici
rappresentano la medesima relazione, devono coincidere una volta che x e $b$ vengano scambiati. Ma trasformare
un punto in un sistema
cartesiano con le coordinate $(x,b)$ in un punto con le coordinate (b,x) significa una simmetria rispetto alla prima bisettrice,
cioè
alla retta passante per l'origine con coefficiente angolare $45^\circ$ sulla quale b=x. Concludiamo che il grafico della funzione logaritmo
si ottiene
dal grafico della funzione esponenziale con una simmetria rispetto alla prima bisettrice.
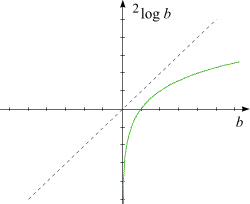
I due schizzi lo illustrano per la base $a=2$ (la bisettrice è tratteggiata). I grafici per altre basi ${a>1}$ sono simili.
Basi speciali
Alcune basi si usano più frequentemente:
- Il logaritmo in base 10 si indica con lg, a volte anche con log (senza menzionare la base). Viene utilizzato quando in un problema compaiono numeri di ordine di grandezza diversa.
- Il logaritmo in base $e$ si chiama logaritmo naturale e si indica con ln (logaritmo naturalis). In alcuni computer viene però indicato con il simbolo log (senza menzionare la base). Lo si usa per descrivere processi di crescita o decadimento. Per calcolare il logaritmo naturale con l'ausilio del calcolatore di log si inserisca il carattere E nella casella per la base.
- Il logaritmo in base 2 viene usato spesso quando si parla del concetto di informazione. Anche per esso a volte si usa il simbolo log (senza menzionare la base), più raramente il simbolo ld (logaritmo dualis).
Come vedete il simbolo "log" può avere diversi significati. Quando lo si incontra in un testo o in uno strumento di calcolo, bisogna sempre accertarsi di quale logaritmo si tratta.
Regole per il calcolo del logaritmo
La definizione del logaritmo può essere riassunta nell'identità
| $${\log_a\, a^x = x}$$ | (20) |
Quando un numero (indicato con $b$ nella definizione di cui sopra) può essere scritto come ${a^x}$, il suo logaritmo (in base $a$) è uguale a $x$. Qui vediamo di nuovo il ruolo del logaritmo come esponente. Se poniamo x=1, abbiamo l'identità ${log_{a}}$ a=1:
La regola principale nell'uso dei logaritmi deriva immediatamente dall'identità (1) per le potenze (la quale, come abbiamo visto sopra, vale anche per esponenti reali). Vediamo come si ricava: fissiamo innanzitutto una base ${a>0 (a\ne 1)}$. Inoltre consideriamo due numeri positivi arbitrari $b, c$ e indichiamo i loro logaritmi con ${x=log_a\,b}$ e ${y=log_a\,c}$. Ciò significa che, scritti come potenze di $a$, i nostri numeri hanno la forma ${b=a^x}$ e ${c=a^y}$. Adesso calcoliamo il loro prodotto ${bc=a^x a^y}$ usando la regola (1) e otteniamo ${a^{x+y}}$. Ma anche questa è una potenza di $a$, e il suo logaritmo è uguale all'esponente ${x+y}$, che a sua volta coincide con la somma dei logaritmi di $b$ e $c$. Concludiamo dunque
| $${\log_a(bc)=\log_a b+\log_a c}$$ | (21) |
per tutti i ${b,c>0}$. In parole: il logaritmo di un prodotto è uguale alla somma dei logaritmi. Possiamo considerare questa identità
come
"l'inverso" della regola (1), ed è su questa che si fonda l'importanza del logaritmo.
Altre due
regole:
| $${log_a(b^k)=k\ log_a b}$$ | (22) |
| $${log_a\,\left(\frac{b}{c}\right)=log_a\, b-log_a\, c}$$ | (23) |
per ogni ${b,c>0}$ e $k$ un numero reale arbitrario. Come caso particolare troviamo (ponendo ${k=-1}$ nella prima oppure ${b=1}$ nella seconda identità)
| $${log_a\,\left(\frac{1}{b}\right)=log_{-a}\, b}$$ | (24) |
per ogni ${b>0}$. Queste regole vi sembreranno più naturali se proverete a verificarle in base dieci con potenze "rotonde" di dieci. Ad esempio ${lg 100=2}$ (il "numero di zeri") e ${lg 1000=3}$, quindi ${lg 100000=5=2+3}$. In questo esempio l'identità (21) si riduce a contare gli zeri.
Adesso siamo in grado di semplificare espressioni contenenti logaritmi.
Esempio: Si semplifichi l'espressione ${log_2(10x)^{-2}log 40}$
- Metodo 1: ${log_2(10x)\log_2 40=}$ applicando (23) ${=log_2(\frac{10x}{40}=log_a(\frac{x}{4}=log_2(2^{-2}x)=}$ applicando (21) ${log_2 x+\log_2(2^{-2})=}$ applicando (20) o (22) ${=log_2 x-2}$.
- Metodo 2:
La differenza fra le due espressioni è quindi ${log_2 x-2}$.
Equazioni esponenziali e logaritmiche
Il concetto di logaritmo ci permette di risolvere problemi che si presentano tipicamente in connessione con processi di crescita o decadimento. Vediamo due esempi:
Esempio 1: Una colonia composta inizialmente da 1000 batteri cresce esponenzialmente e raddoppia la sua grandezza ogni ora. Quando
conterrà 7000 batteri?
Il numero di batteri dopo t ore è pari a ${1000 \cdot 2^t}$. Chiedere quando ci saranno 7000 batteri da luogo all'equazione
${1000 \cdot 2^t=7000}$?, da risolvere
per $t$. Intanto la semplifichiamo:
| $${2^t=7}$$ | (25) |
Per risolverla, possiamo scegliere uno dei seguenti metodi:
- Metodo 1: Usiamo la definizione di cui sopra del logaritmo e concludiamo che (l'unica) soluzione è ${t=\log_2 7 \approx 2.807}$.
- Metodo 2: Vogliamo impiegare il logaritmo in base 1 senza tirare in ballo il logaritmo in base 2. Il metodo standard consiste nell'applicare sull'equazione (25) il logaritmo in base dieci lg. Poichè il logaritmo è una funzione invertibile, così facendo trasformiamo (25) in un'equazione equivalente
| $${lg\,(2^t)=\lg\, 7}$$ | (26) |
Applicando la regola (22) possiamo semplificare così:
| $${t\, lg\, 2=lg 7}$$ | (27) |
e la soluzione è ${t=\frac{lg\, 7}{lg\, 2} \approx 2.807}$ (che naturalmente coincide con ${log_2 7}$). Questo metodo può sembrare
complicato, ma in realtà è più
semplice nell'applicazione. L'idea è di estrarre l'incognita dall'esponente applicando il logaritmo
(in una base qualsiasi) su entrambi le parti dell'equazione.
La soluzione è quindi: dopo 2807 ore (cioè 2 ore e 48.4 minuti) ci saranno 7000 batteri.
Vedi la lezione sulle trasformazioni equivalenti
Esempio 2: L'intensità di una sostanza radioattiva dopo 5 anni scende a ${\frac{1}{3}}$ del valore iniziale. Si determini il tempo di dimezzamento, cioè il tempo necessario affinchè l'intensità sia dimezzata. Sappiamo in generale che l'intensità dopo $t$ anni diminuisce del fattore ${2^{-\frac{t}{s}}}$ dove $s$ è il tempo di dimezzamento misurato in anni. Dopo 5 anni questo fattore è pari a ${2^{-\frac{5}{s}}}$. D'altra parte sappiamo che il suo valore deve essere ${\frac{1}{3}}$. Questo dà luogo all'equazione:
| $${2^{-\frac{5}{s}}=\frac{1}{3}}$$ | (28) |
che risolviamo per $s$. Scegliamo il logaritmo naturale e lo applichiamo su entrambi i lati dell' equazione per ottenere
| $${ln\,(2^{-\frac{5}{s}})=\ln\,\left(\frac{1}{3}\right)}$$ | (29) |
Applicando la (22) a sinistra e la (24) a destra abbiamo
| $${-\left(\frac{5}{s}\right)ln\, 2=-ln\, 3}$$ | (30) |
Possiamo risolvere questa equazione per $s$: il tempo di dimezzamento è ${s=5\frac{ln 2}{ln 3} \approx 3.155}$ anni.
Nelle equazioni
(25) e (28) l'incognita si trovava nell'esponente e abbiamo usato il logaritmo come mezzo per
estrarla. A volte si hanno anche
equazioni come
| $${lg\,(x^2)=2\,lg\,(x+1)}$$ | (31) |
che contengono già logaritmi. Per risolvere questo tipo di equazioni, cominciamo con l'osservare che hanno soltanto un senso quando ${x^2}$ e ${x+1}$ sono entrambi positivi. L'insieme di definizione dell'equazione è quindi ${ \{x\in R\mid x>-1$ e $x\ne 0\}}$. Possiamo trovare la soluzione applicando la regola (22) al membro destro per ottenere
| $${lg\,(x^2)=\lg\,(x+1)^{2}}$$ | (32) |
Poichè il logaritmo è una funzione iniettiva, gli argomenti devono coincidere:
| $${x^2=(x+1)^2}$$ | (33) |
e, togliendo le parentesi, otteniamo un'equazione lineare con la soluzione ${x=-\frac{1}{2}}$. Dato che si tratta di un valore contenuto
nell'insieme di definizione,
abbiamo dunque trovato l'(unica) soluzione dell'equazione (31).
Per completezza
dobbiamo aggiungere che non tutte le equazioni contenenti
potenze o logaritmi dell'incognita possono essere risolte con queste tecniche.
Può capitare che un'equazione del genere abbia una soluzione, ma che questa non possa
essere espressa con i metodi che conosciamo. In tal
caso non ci resta che applicare metodi grafici o numerici.
Un esempio è l'equazione ${2^x=-x}$. Si tenti di osservare una soluzione
approssimata.